¡Calcula al instante online! Tu asistente matemático para calcular el volumen de una esfera de forma fácil.
Calculadora Volumen Esfera
Volumen:
0.00
¿Quieres ver otras herramientas de cálculo?
La siguiente calculadora online es una herramienta para calcular el volumen de una esfera, basado en el radio de la esfera. La aplicación calcula el volumen de la esfera utilizando la fórmula de Volumen = (4/3) × π × radio³. Esto permite calcular el volumen de cualquier esfera, ya sea pequeña o grande.
Además, como opcional, la calculadora de volumen de una esfera también permite calcular su capacidad a partir del diámetro y de su circunferencia.
¿Cómo funciona la calculadora de volumen de una esfera?
Para calcular el volumen de la esfera, sigue estos pasos:
- Ingresa el valor del radio (r):
- Introduce el radio de la esfera en el campo indicado y selecciona la unidad de dimensión si es necesario. Opcionalmente, puedes usar el diámetro y circunferencia para calcular el espacio interior de la esfera.
- Calcular volumen de la esfera:
- La calculadora realizará el cálculo automáticamente y mostrará el volumen de la esfera según la unidad seleccionada.
Recordamos que las fórmulas para calcular el volumen esférico son varias según la distancia a utilizar:
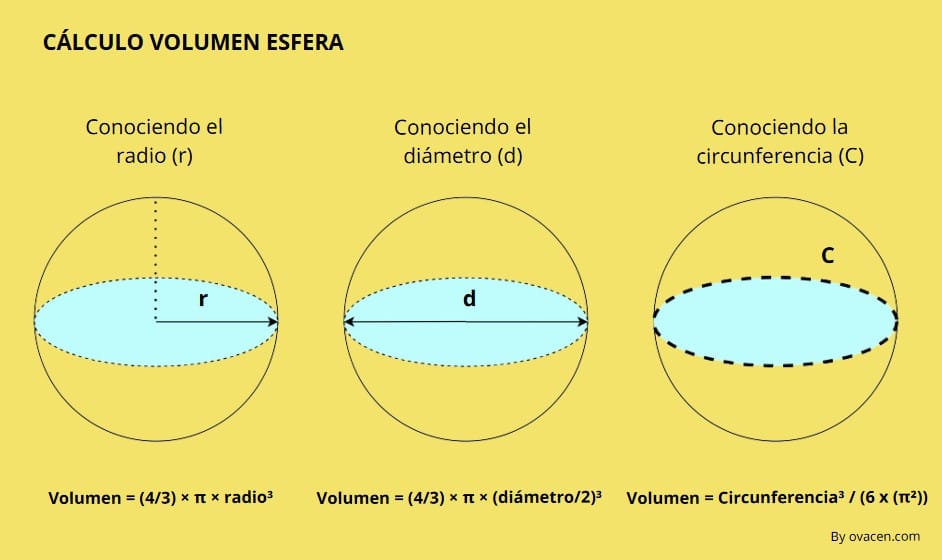
El volumen de una esfera se mide en unidades cúbicas, como metros cúbicos (m³), centímetros cúbicos (cm³) o pulgadas cúbicas (in³). Y la formula para calcular el volumen es:
- Formula para calcular el volumen de una esfera con el radio: Volumen = (4/3) × π × radio³
- Formula para calcular el volumen de una esfera con el diámetro: Volumen = (4/3) × π × (diámetro/2)³
- Formula para calcular el volumen de una esfera con la circunferencia: Volumen = Circunferencia³ / (6 x (π²))
🟧 Nota: La fórmula para calcular el volumen de una esfera es universal, y recordemos que Número pi = π aproximadamente es 3.1416
Ejemplo de cálculo del volumen de una esfera:
- Si tenemos una esfera con un radio de 5 cm, aplicaríamos el siguiente cálculo: Volumen = (4/3) × π × (5 cm)³ ≈ 523.6 cm³.
- Si conocemos el diámetro de una esfera, por ejemplo, 10 cm, primero dividimos el diámetro entre 2 para obtener el radio (5 cm). Aplicamos la fórmula para calcular el volumen y obtenemos el mismo resultado de 523.6 cm³.
También aportamos el siguiente video educativo para aprender tanto la fórmula matemática, conceptos de geometría, la diferencias entre superficie y volumen o cómo sacar el volumen de una esfera:
Es importante destacar que el volumen de una esfera es exactamente dos tercios del volumen del cilindro circunscrito (el cilindro más pequeño que puede contener la esfera).
¿Qué unidades puedes utilizar en la calculadora para calcular el volumen de una esfera?
La calculadora para obtener la capacidad de una esfera permite ingresar los valores en las siguientes unidades:
- Milímetros (mm) → Milímetros Cúbicos (mm³)
- Centímetros (cm) → Centímetros Cúbicos (cm³)
- Metros (m) → Metros Cúbicos (m³)
- Kilómetros (km) → Kilómetros Cúbicos (km³)
- Pulgadas (in) → Pulgadas Cúbicas (in³)
- Pies (ft) → Pies Cúbicos (ft³)
- Yardas (yd) → Yardas Cúbicas (yd³)
- Millas (mi) → Millas Cúbicas (mi³)
Puedes calcular el volumen, siempre que los valores de entrada sean positivos. Además, puedes cambiar las unidades de entrada y salida para adaptarlas al sistema métrico o imperial.
En la vida real, aunque no lo parezca, se utiliza bastante la formula para calcular el volumen esférico: Desde ingeniería para depósitos a arquitectura con las cúpulas geodésicas, en astronomía para los planetas, en diseño industrial, etc.
🟧 Nota: Si tienes alguna duda sobre la aplicación online para calcular el volumen de esferas, no dudes en consultarnos desde el apartado de contacto en el pie de página.
Preguntas frecuentes sobre el volumen de una esfera – FAQ
¿Qué es el volumen de una esfera?
El volumen de una esfera es la cantidad de espacio que ocupa un objeto tridimensional perfectamente redondo. Se mide en unidades cúbicas y se calcula utilizando la fórmula de Volumen = (4/3) × π × radio³.
¿Cuál es la fórmula para calcular el volumen de una esfera?
La fórmula para calcular el volumen de una esfera es: Volumen = (4/3) × π × radio³, donde π (pi) ≈ 3.1416 y el radio es la distancia desde el centro de la esfera hasta su superficie.
¿Qué unidades se usan para medir el volumen de una esfera?
El espacio interior de una esfera se mide en unidades cúbicas, utilizando como ejemplo los milímetros cúbicos (mm³), centímetros cúbicos (cm³), metros cúbicos (m³), pulgadas cúbicas (in³), etc.
¿Cómo se calcula el volumen de una esfera si solo tengo el diámetro?
Si tienes el diámetro de la esfera, primero divide el diámetro entre 2 para obtener el radio. Luego, usa la fórmula para el volumen esférico de = (4/3) × π × radio³.
¿Cómo afecta el tamaño del radio al volumen de la esfera?
El volumen de una esfera aumenta exponencialmente con el radio, ya que el radio se eleva al cubo en la fórmula. Por ejemplo, al duplicar el radio aumenta el volumen por un factor de 8.
¿Qué sucede si la esfera es hueca?
Si la esfera está hueca (es decir, tiene un vacío interno), calcula el volumen externo y resta el volumen interno utilizando los cálculos matemáticos de Volumen hueco = Volumen externo – Volumen interno.
¿Para qué sirve saber calcular el volumen de una esfera?
El cálculo del volumen de una esfera es útil en diferentes campos como la ingeniería (volumen de tanques esféricos), en la astronomía (volumen de planetas y estrellas), en el diseño de recipientes (bolas, envases), en física, matemáticas, etc.
¿Cuál es la diferencia entre el volumen de una esfera y su área superficial?
El volumen mide la cantidad de espacio tridimensional dentro de la esfera, mientras que el área de superficie mide el espacio bidimensional, en 2D, que cubre la esfera. La fórmula del área de superficie de una esfera es: Área = 4 × π × radio².
¿Cuál es la diferencia entre una esfera perfecta y otras formas redondeadas?
Una esfera perfecta tiene todas las superficies equidistantes de su centro. Otras formas redondeadas, como elipsoides o esferoides, tienen dimensiones desiguales, y no se puede usar la fórmula estándar para calcular su volumen.
¿Puedo calcular el volumen de una esfera si solo conozco su área superficial?
Directamente No. El área superficial y el volumen son propiedades diferentes de una esfera, y no se puede calcular una a partir de la otra sin conocer alguna otra medida, como por ejemplo el radio.
¿Qué valor de π (pi) debo usar para calcular el volumen de una esfera?
Normalmente para cálculos generales, se usa π ≈ 3.1416, y para una mayor precisión π ≈ 3.14159265. Algunas calculadoras online científicas permiten usar π con más decimales automáticamente.
¿Qué pasa si la esfera no es completamente sólida?
Si la esfera tiene huecos o espacios no sólidos, se deberá restar el volumen de esos espacios al total utilizando mediciones precisas.
