El teorema de Pitágoras establece que en un triángulo rectángulo, la suma de los cuadrados de los catetos (lados que forman el ángulo recto) es igual al cuadrado de la hipotenusa (lado opuesto al ángulo recto y más largo). Fórmula de Pitágoras es: a² + b² = c² (a y b son catetos, y c es hipotenusa)
- Catetos: Los dos lados que forman el ángulo recto (lados perpendiculares)
- Hipotenusa: El lado opuesto al ángulo recto (lado más largo)
- Triangulo rectángulo: La ecuación pitagórica solo aplica a triángulos que tienen un ángulo de 90 grados.
¿Quieres resolver problemas matemáticos y geométricos de la relación pitagórica? Mira la calculadora online para resolver el Teorema de Pitágora (hipotenusa) de forma fácil.
¿Quieres ver otras herramientas de cálculo?
Esta calculadora online sirve para aplicar el Teorema Pitágoras y encontrar el valor de la hipotenusa (c – lado más largo) en un triángulo rectángulo. Para el cálculo, solo tienes que introducir las longitudes de los dos catetos (a y b – lados perpendiculares) y pinchar en calcular. El resultado se mostrará automáticamente.
El Teorema de Pitágoras es una fórmula fundamental en geometría que se aplica a los triángulos rectángulos , es decir, triángulos que tienen un ángulo de 90° (ángulo recto).
¿Cómo calcular el Teorema de Pitágoras?
Para aplicar Pitágoras y calcular la hipotenusa (c) de un triángulo rectángulo. La formulación es: a² + b² = c². Entonces, de la ecuación pitagórica podemos extraer que c = √(a² + b²), siendo que a y b son los catetos que forman el ángulo recto.
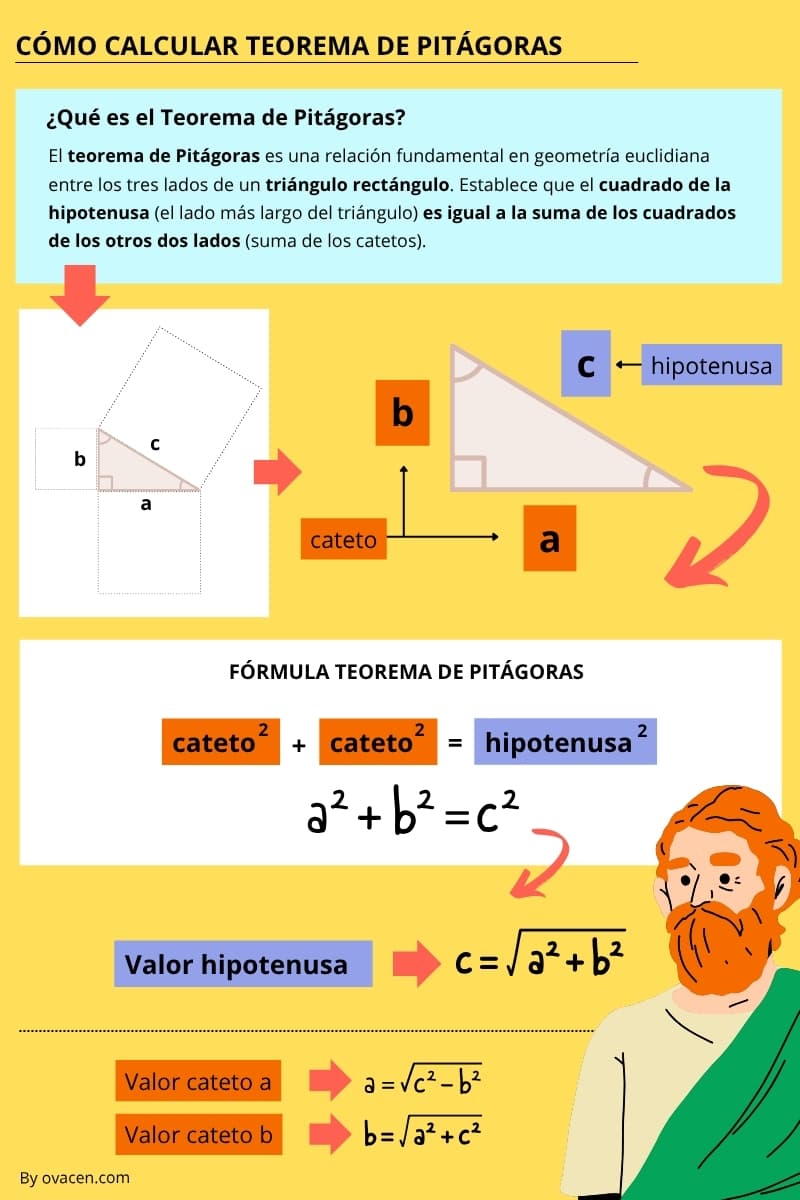
Con todas estas formulas tienes la base matemática para hacer cálculos en aplicaciones geométricas o una calculadora de hipotenusa y catetos útil.
Algunos cálculos de ejemplos teorema de Pitágoras:
- Ejercicio 1. Imagina que tienes un triángulo rectángulo donde un cateto mide 3 centímetros y el otro mide 4 centímetros… ¿Cuál sería el valor de la hipotenusa, del lado más largo? Podríamos hacer los siguientes cálculos:
-
- Cuadrado del primer cateto: 3×3 = 9 cm (Valor cateo a)
- Cuadrado del segundo cateto: 4×4 = 16 cm (Valor cateo b)
- Ahora, sumamos esos resultados: 9+16 = 25 cm (Valor de hipotenusa)
- Si aplicáramos la ecuación directa sería: Hipotenusa = √ (a² + b²), es decir, Hipotenusa = √ (3² + 9²) = 25 cm
-
- Ejercicio 2: Tenemos un triángulo rectángulo, la hipotenusa mide 10 m y un cateto mide 6 m… ¿Cuál es el valor del otro cateto (b)?
-
- Si nos basamos en el teorema de pitágora (a² + b² = c²) y despejamos la b para realizar los cálculos, obtenemos que el cateto b = √ (a² + c²)
- Los cálculos serían: b = √ (6² + 10²) = 8 cm el valor del cateto.
-
🟧 Historia Teorema Pitágoras: Aunque se atribuye al filósofo y matemático griego Pitágoras (siglo VI a.C). El conocimiento y uso práctico de esta relación ya existían miles de años antes. Civilizaciones antiguas como la babilónica, egipcia y china lo aplicaban desde aproximadamente el 2000 a.C., como en la tablilla Plimpton 322 de los babilonios, que lo utilizaban con fines prácticos en construcción y topografía.
Recuerda que el teorema de Pitágoras solo aplica a triángulos rectángulos (llama también el teorema de los tres cuadrados), pero es una herramienta fundamental en geometría, trigonometría, física, ingeniería, construcción y muchas disciplinas científicas. ¿Te atreves con el siguiente cuestionario de ejercicios?
Cuestionario: Teorema de Pitágoras
Ejercicio 1: Encuentra la hipotenusa
Un triángulo rectángulo tiene catetos de 3 cm y 4 cm.
¿Cuánto mide la hipotenusa?
cm
Ejercicio 2: Encuentra un cateto
Un triángulo rectángulo tiene una hipotenusa de 10 cm y un cateto de 6 cm.
¿Cuánto mide el otro cateto?
cm
Ejercicio 3: Triángulo isósceles rectángulo
Un triángulo rectángulo tiene dos catetos iguales de 7 cm cada uno.
¿Cuánto mide la hipotenusa? (redondea a 1 decimal)
cm
Ejercicio 4: Problema práctico
Una escalera de 5 metros se apoya contra una pared. Si la base de la escalera está a 3 metros de la pared, ¿a qué altura toca la pared?
metros
Ejercicio 5: Diagonal de un rectángulo
Un rectángulo tiene dimensiones de 12 cm × 9 cm.
¿Cuánto mide su diagonal?
cm
Ejercicio 6: Verificación de triángulo rectángulo
¿Es rectángulo un triángulo con lados de 5, 12 y 13 unidades?
Ejercicio 7: Distancia entre puntos
¿Cuál es la distancia entre los puntos A(1, 2) y B(4, 6) en un plano cartesiano?
(redondea a 1 decimal)
unidades
¡Curiosidad! El Teorema de Gougu (en Asia Oriental): En algunas culturas asiáticas, especialmente la china, este teorema fue descubierto y formulado de forma independiente mucho antes de Pitágoras, y se le conoce por este nombre.
Usos del teorema de Pitágoras
Este teorema es una de las fórmulas matemáticas más aplicadas siendo una herramienta crucial en diversos campos:
- Arquitectura, ingeniería, construcción o diseño: Es fundamental para calcular distancias, alturas, pendientes, asegurar ángulos rectos precisos en estructuras y en el diseño de edificios, puentes y rampas.
- Topografía, geodesia y navegación: Esencial para determinar distancias horizontales y verticales en levantamientos topográficos, para mapas, cálculo de rutas, inclinaciones de terrenos y es la base de sistemas de medición como el GPS.
- Física: Utilizado para calcular la magnitud resultante de vectores, la descomposición de fuerzas y el cálculo de trayectorias.
- Informática y ciencias de la Información: Sus principios se aplican en conceptos abstractos para calcular distancias en espacios multidimensionales, relevante en áreas como el reconocimiento facial en inteligencia artificial.
🟧 Nota: Nuestra calculadora del Teorema de Pitágoras también permite realizar cálculos inversos si conoces la hipotenusa y uno de los catetos, además tendrás una representación geométrica del triangulo rectángulo obtenido.
Ejemplos precalculados del Teorema de Pitágoras
A continuación, te ofrecemos una tabla con algunos pares de catetos y sus respectivas hipotenusas ya calculadas:
| Cateto a (vertical) | Cateto b (horizontal) | Hipotenusa c |
|---|---|---|
| 0.3 | 0.4 | 0.5 |
| 1 | 1 | ≈1.414 |
| 2 | 2 | ≈2.828 |
| 2.5 | 6 | ≈6.5 |
| 3 | 4 | 5 |
| 3.5 | 12 | ≈12.5 |
| 4.5 | 6 | ≈7.5 |
| 5 | 12 | 13 |
| 5.5 | 13.2 | ≈14.3 |
| 6 | 8 | 10 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 12 | 15 |
| 9 | 40 | 41 |
| 10 | 10 | ≈14.142 |
| 11 | 60 | 61 |
| 12 | 16 | 20 |
| 14 | 48 | 50 |
| 15 | 20 | 25 |
| 16 | 30 | 34 |
| 18 | 24 | 30 |
| 20 | 21 | 29 |
| 7.5 | 10 | ≈12.5 |
| 9.9 | 13.2 | ≈16.5 |
🟧 Cualquier otra duda sobre la calculadora o cálculos sobre la formula de hipotenusa o el teorema de los tres cuadrados puedes consultarnos desde el apartado de contacto en el pie de página.
Preguntas frecuentes sobre el Teorema de Pitágoras – FAQ
¿Qué es el teorema de Pitágoras?
El teorema de Pitágoras es una fórmula matemática que se usa para encontrar la longitud de un lado en un triángulo rectángulo cuando se conocen las longitudes de los otros dos lados. La ecuación es a² + b² = c², donde «a» y «b» son los catetos y «c» es la hipotenusa.
¿Para qué sirve el teorema de Pitágoras?
Sirve principalmente para resolver problemas con triángulos rectángulos, como encontrar la longitud de un lado desconocido. También tiene aplicaciones prácticas en construcción, navegación, diseño y muchas áreas de la física e ingeniería.
¿Cómo se aplica el teorema de Pitágoras?
Se aplica elevando al cuadrado las longitudes de los dos catetos, sumándolos y luego sacando la raíz cuadrada del resultado para obtener la hipotenusa. Si se busca un cateto, se resta el cuadrado del otro cateto del cuadrado de la hipotenusa y luego se saca la raíz cuadrada.
¿Cuál es la fórmula del teorema de Pitágoras?
La fórmula es a² + b² = c², donde a y b representan los catetos del triángulo rectángulo y c representa la hipotenusa, que es el lado más largo y opuesto al ángulo recto.
¿Cómo sabes si un triángulo es rectángulo usando el teorema de Pitágoras?
Si al aplicar la fórmula a² + b² = c² con las medidas del triángulo, la igualdad se cumple, entonces el triángulo es rectángulo. Si no cumple, no lo es.
¿Funciona el teorema de Pitágoras en cualquier triángulo?
No, solo funciona en triángulos rectángulos, que tienen un ángulo de 90 grados. Si el triángulo no es rectángulo, la fórmula no aplica.
¿Cómo sabes cuál es la hipotenusa en un triángulo rectángulo?
La hipotenusa es siempre el lado más largo del triángulo rectángulo y está frente al ángulo de 90 grados. Los otros dos lados, son los catetos.
¿Cómo encontrar la hipotenusa con el teorema de Pitágoras?
Para encontrar la hipotenusa, se elevan al cuadrado las longitudes de los dos catetos, se suman y luego se le aplica la raíz cuadrada al resultado. Así obtenemos la longitud de la hipotenusa.
¿Cómo encontrar un cateto con el teorema de Pitágoras?
Para encontrar un cateto desconocido, se eleva al cuadrado la hipotenusa, se resta el cuadrado del otro cateto conocido y luego se aplica la raíz cuadrada del resultado.
¿Por qué es importante el teorema de Pitágoras?
Es importante porque es una herramienta fundamental en geometría y trigonometría. Permite resolver problemas relacionados con distancias y ángulos, y tiene múltiples aplicaciones en ciencia, tecnología, ingeniería y arte.
¿Quién inventó el teorema de Pitágoras?
Aunque el teorema lleva el nombre del filósofo griego Pitágoras, quien vivió alrededor del siglo VI a.C., hay evidencia de que civilizaciones anteriores, como los babilonios y los egipcios, ya usaban esta relación entre los lados de un triángulo rectángulo.
¿Qué es un triángulo pitagórico?
Es un triángulo rectángulo cuyos lados tienen longitudes que son números enteros y cumplen con a² + b² = c². Un ejemplo clásico es el triángulo de lados 3, 4 y 5, porque 3² + 4² = 9 + 16 = 25 = 5²
