Find the area of a triangle? Your math assistant to calculate the area of triangle (calculate a triangle?) easily and quickly.
Triangle Area Calculator
Area:
0.00
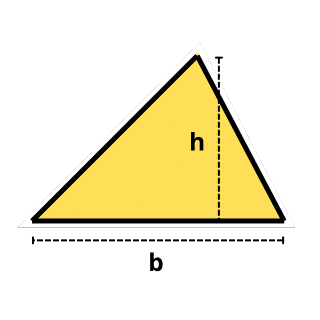
A = (b × h) ÷ 2
Area:
0.00
A = √s(s-a)(s-b)(s-c), where s = (a+b+c)÷2
°
Area:
0.00
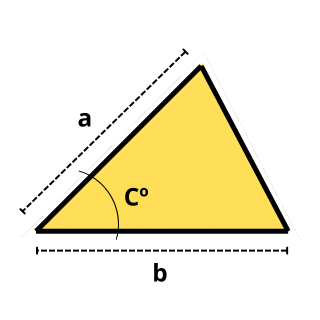
A = (1/2) × a × b × sin(C)
°
°
Area:
0.00
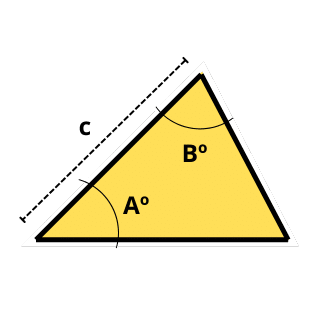
A = (1/2) × c² × sin(A) × sin(B) ÷ sin(A+B)
°
°
°
Area:
0.00
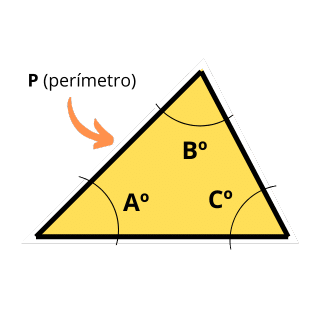
A = (P²/4) × sin(A) × sin(B) × sin(C) / sin(A+B+C)
Do you want to see other calculation tools?
The following online calculation application is a tool to calculate the area of a triangle, based on the base and height. Calculate the extension of the triangle using the formula Triangle area = (base × height) / 2, it can be used for both small and large elements.
Additionally, optionally, it allows calculating the triangular surface by knowing other data that we explain now.
How does the triangle area calculator work?
The process to use the triangle area calculator is simple and fast:
- Enter data:
- You must enter the values of the base (b) and the height (h) in the corresponding fields.
- You can select the unit of measurement (cm, m, etc).
- Area calculation:
- The calculator applies the formula for the area of a triangle: A = (b × h) / 2
- Once the values are entered, the area is displayed automatically.
- Additional calculation options:
- Below the calculator, there are alternative options to calculate the surface in case you do not have the base and height directly:
- Option: Calculate the area of the triangle with three sides of the triangle, you can use the Heron’s formula.
- Option: Calculate the area of the triangle with two sides and the angle between them, you can use the formula Area = (1/2) × a × b × sin(C), where C is the angle in degrees.
- Option: Calculate the area of the triangle with two angles and one side. It would involve first calculating the third angle and then using the law of sines to find the remaining sides
- Option: Calculate the area of the triangle with the three angles and the perimeter of the triangle. The perimeter is used to calculate a side and then apply the law of sines.
- Below the calculator, there are alternative options to calculate the surface in case you do not have the base and height directly:
Remember! Heron’s formula allows you to calculate the area of a triangle knowing only the length of its three sides
You can calculate the surface of the triangle as long as the input values are positive. Additionally, you can change the input and output units to adapt them to the metric or imperial system.
The application facilitates the calculation of the area of a triangle in a simple way and also provides additional methods according to the information available to the user.
How to calculate the area of a triangle?
We remind you that the triangle area formula is: Area = (base × height) / 2, and it works for any triangle (scalene, isosceles, equilateral).
It is important to remember that the calculations of the Triangle surface = (base × height) / 2, work for any type of triangle, whether scalene, isosceles, equilateral.
However, if we do not know the base and height, there are other options. The formula for surface area of a triangular prism and its variants are:
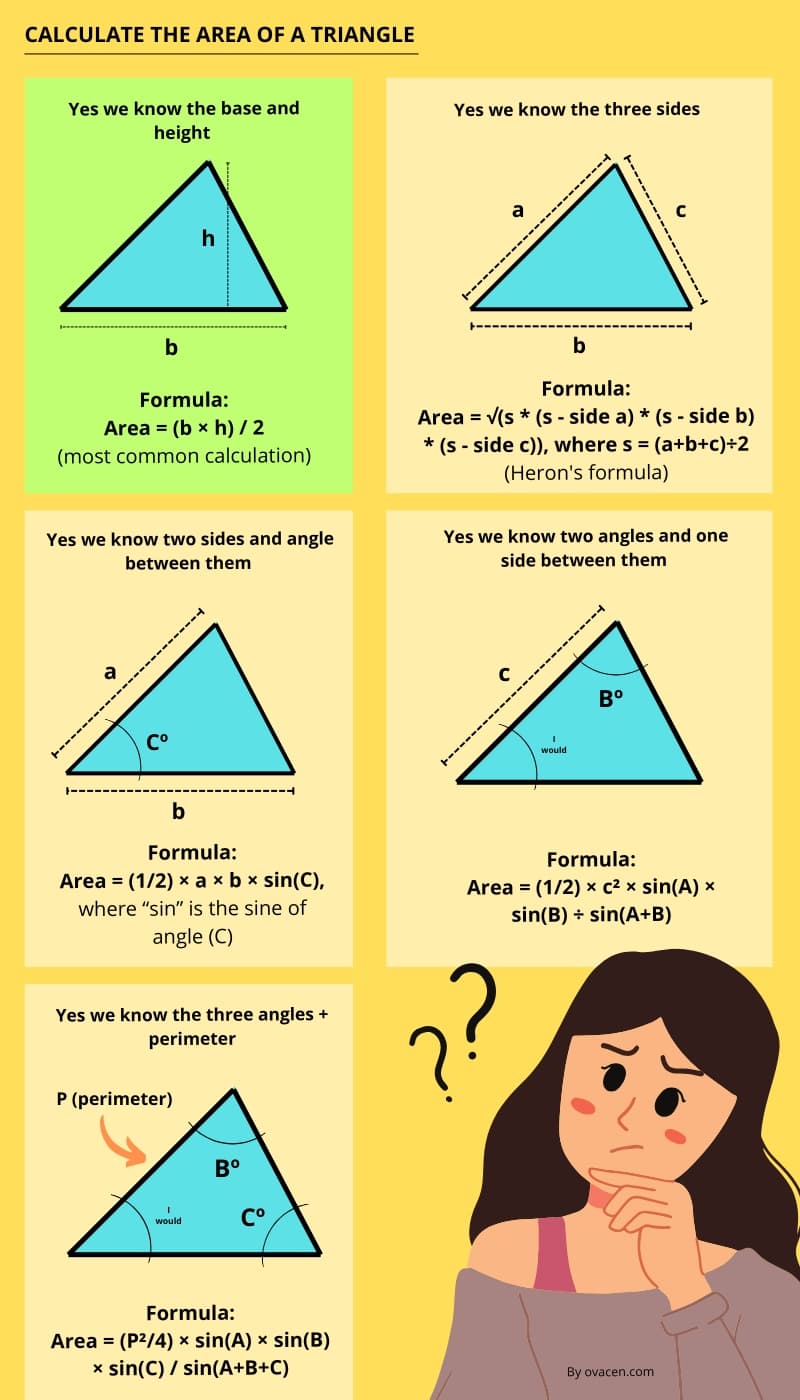
- If we know the base and height of the triangle. Formula triangle area = (b × h) / 2.
- Example: you have a triangle with a base of 10 cm and a height of 12 cm. To find the area, simply multiply the base by the height and divide the result by two. The calculation would be: Triangle area = (10×12) / 2 = 60.
- If we know the three sides of the triangle. Area Formula = √(s * (s – side a) * (s – side b) * (s – side c)), where s = (a+b+c) / 2 (Heron’s formula).
- If we know two sides and the angle between them of the triangle. Area Formula = (1/2) × a × b × sin(C), where “sin” is the sine of the angle (C).
- If we know two angles and a side between them of the triangle. Area Formula = (1/2) × c² × sin(A) × sin(B) / sin(A+B)
- If we know the three angles plus the perimeter of the triangle. Area Formula = (P²/4) × sin(A) × sin(B) × sin(C) / sin(A+B+C)., where “sin” is the sine of the corresponding angle.
🟧 Note: If you have any questions about calculator for triangle area, do not hesitate to contact us from the contact section in the footer.
Frequently asked questions about the area of a triangle – FAQ
How to calculate the area of a triangle?
To obtain the area of a triangle, use the formula: Area = (base x height) / 2. Where the “base” is the length of one of the sides, and “height” is the perpendicular distance from the base to the opposite vertex.
How to calculate the surface of a triangle?
To obtain the surface of a triangle, use the formula: Area = (base x height) / 2. Where the “base” is the length of one of the sides, and “height” is the perpendicular distance from the base to the opposite vertex.
What do I need to calculate the area of a triangle?
You need to know the length of the base (b) and the height (h), which is a perpendicular line from the base to the opposite vertex.
How to calculate the area of a right triangle?
To know the surface of a right triangle, use the formula: Area = (base × height) / 2, remember that the “base” is the length of one of the sides, and “height” is the perpendicular length from the base to the opposite vertex.
How do I calculate the area of an equilateral triangle?
You can use the formula: Area = (side² x √3) / 4. Where “side” is the length of any of the sides of the triangle.
How do I find the height of a triangle if it’s not given?
It depends on the type of triangle: for a right triangle, the height can be one of the legs. And for an isosceles or scalene triangle, you can use the Pythagorean theorem if you know the lengths of the sides, or trigonometry if you know the angles.
How do I calculate the area if given base 6 and height 4?
Apply the formula: A = (6 × 4) / 2 = 24 / 2 = 12 square units.
What do I do if the height is not given to calculate the surface of a triangle?
If you have the sides and it is a right triangle, use one side as the base and the other as the height. If not, you need more data or use another formula like Heron’s.
Can the area of a triangle be calculated if I only know the angles?
No, you need at least the length of one of the sides or the perimeter of the triangle. The angles determine the shape, but not the size.
What is Heron’s formula?
Heron’s formula is used to calculate the surface of a triangle when its three sides (a, b, c) are known. First, calculate the semi-perimeter: s = (a + b + c) / 2, and then Area = √[s (s – a)(s – b)(s – c)]. For example: if the side dimensions are 3, 4, 5; then s = 12 / 2 = 6; and the Area = √[6 (6-3)(6-4)(6-5)] = √(632*1) = √36 = 6.
Can I calculate the area of a triangle with two sides and the angle between them?
Yes, use the formula: Area = (1/2) × a × b × sin(C), where a and b are the sides and C is the angle between them. For example, if we know the sides are 5 and 6, and an angle of 30°, then the calculations are A = (1/2) × 5 × 6 × sin(30) = 7.5
What units do I use for the area of a triangle?
It depends on the units of the base and height: if they are in meters, the area will be in square meters (m²); if in centimeters, in cm².
Does the same area formula for a triangle work for all types?
Yes, the calculations of A = (base x height) / 2 work for any triangle (scalene, isosceles, equilateral) as long as you know the base and height.
What is the sine of an angle and how is it used to calculate the area?
The sine is a trigonometric function. The formula Area = (1/2) × a × b × sin(C) is used when you know two sides (a and b) and the angle in degrees (C). The sine of the angle is calculated with a scientific calculator.
